
With enough computer power this is a thing that can be done, but it typically requires more computing power than can reasonably be found in one place. This is really, really not obvious, so be cool.
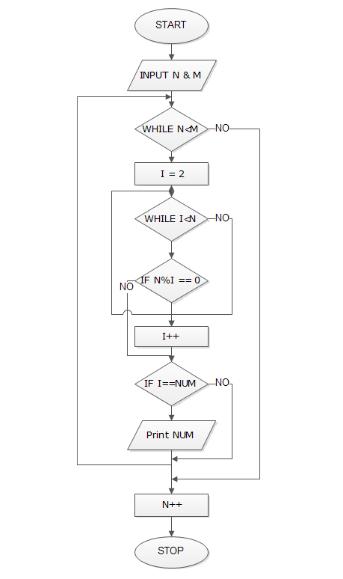
Create the sequence of numbers, S k, defined recursively as S k = (S k-1) 2 – 2 with S 0 = 4. Fortunately, there’s yet another cute trick. Just like FLT there are false positives for example M 11 = 2 11 -1 = 23×89, which is clearly composite even though 11 is prime. Turns out that if n isn’t prime, then neither is M n. The reason that 2 57,885,161 − 1 can be written so succinctly (just a power of two minus one) is that it’s one of the Mersenne primes, which have a couple nice properties that make them easy to check.Ī Mersenne number is of the form M n = 2 n -1. To check that a number this big is prime you need to pick the number carefully. Number of digits in the largest known prime vs. At 17.4 million digits, this number is around ten times longer than the Lord of the Rings, and about twice as interesting as the Silmarillion. The largest prime found to date (May 2014) is N = 2 57,885,161 − 1. Stupid Big (~10 10 10): Even if you have a fantastically fast technique for determining primality, you can render it useless by giving it a large enough number.

The time it takes for both FTL and AKS to work is determined by the log of N (which means they’re fast enough to be useful). But in 2002 Primes is in P was published, which introduced AKS (Agrawal–Kayal–Saxena primality test) that can determine whether or not a number is prime with complete certainty. For most purposes (such as generating encryption keys) FLT is more than good enough.įor a very long time (millennia) there was no way to verify with certainty that a number is prime in an efficient way. However, because of their existence we can’t use FLT with impunity. These are the “ Carmichael numbers” and they’re more and more rare the larger the numbers being considered. This test has no false negatives, but it does sometimes have false positives. Equivalently, it’s the remainder after division by N. “Mod N” means every time you have a value bigger than N, you subtract multiples of N until your number is less than N. Medium (~10 10): Fermat’s Little Theorem or AKS.įermat’s little theorem (as opposed to Fermat’s theorem) works like this: if N is prime and A is any number such that 1

 0 kommentar(er)
0 kommentar(er)
